| Главная » Статьи » Excel » Графики и диаграммы |
Меня трудно чем-то удивить в Excel, но когда я впервые увидел вот этот сайт, то у меня чуть глаз не выпал на клавиатуру. Очень рекомендую вам пройти по ссылке и поглазеть. В моём личном рейтинге эта команда (там двое мужчин и девушка) является №1 в мире по Excel. Сегодня я вам покажу нечто из их арсенала (с моими некоторыми адаптациями). Посмотрим на то, как при помощи точечной диаграммы с гладкими кривыми строить ТАКИЕ сложные вещи, что, когда глядишь на это в первый раз, просто не веришь, что это вообще можно нарисовать в Excel. Ну, например, как вам это: 
Дело в том, что мы все привыкли, что такие графики строятся по точкам, которые рассчитываются в ячейках таблицы. Тут же используется реально очень крутой трюк, который позволяет строить графики любых сложнейших функций, не используя ни диапазоны с точками XY, ни какие-либо макросы. Всё что вам нужно - это точечная диаграмма с гладкими кривыми, несколько констант и несколько именованных формул. Те граждане, кто пока плохо понимает, зачем это всё надо, сейчас просто откроют файлик, включат макросы и нажмут кнопку Старт, потому что это ПРОСТО КРАСИВО. На это можно смотреть минут 15 и всё равно будет интересно. Дольше смотреть не рекомендую, так как глаза и мозг устанут. Смотреть красоту ТУТА с теми, кому интересно, как это устроено, продолжаем разговор. В принципе абсолютно без разницы, какой график строить. Я взял циклоидальные кривые, так как они очень красивы, разнообразны и сложны. Эпициклоиды и гипоциклоиды (подмножество циклоидальных кривых) строятся по следующим параметрическим формулам: 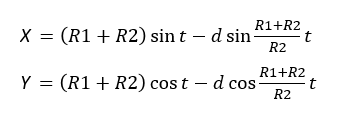
Эпициклоиды строятся так: 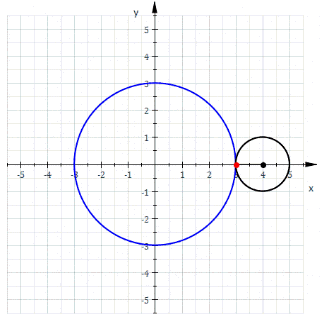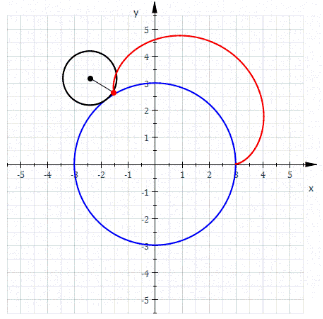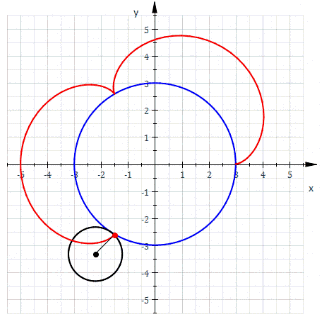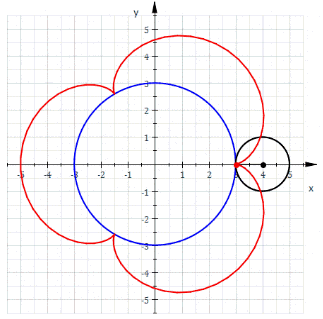
Гипоциклоиды так: 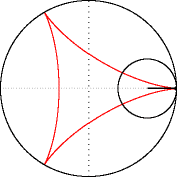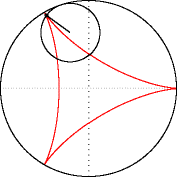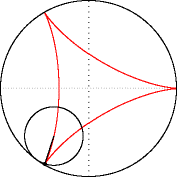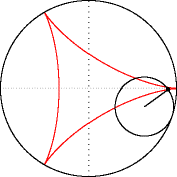
Знаки у R1 и R2 относительно друг друга определяют тип кривой (по какой поверхности круга R1 - по внутренней или внешней - будет катиться круг R2). Обратите внимание, что t - это угод в радианах. Напоминаю, что углы в 5' и 365' - разные углы. Если мы заглянем в ряды данных диаграммы, то увидим это: 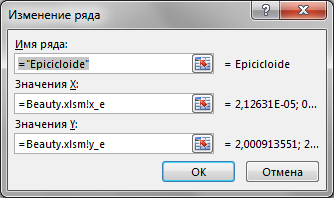
Сердце решения располагается тут: 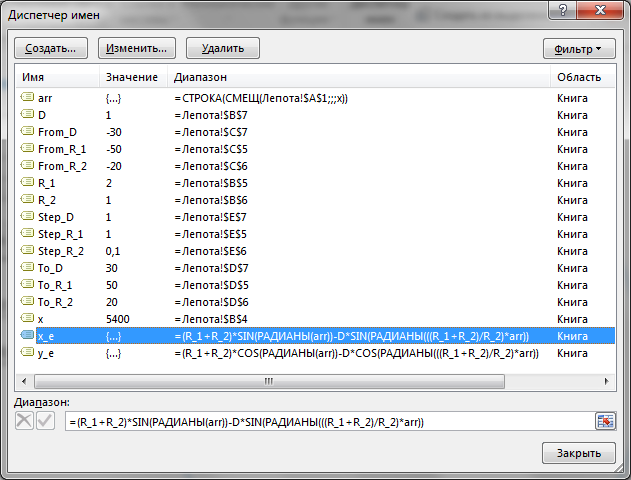
Как видите, большинство именованных диапазонов просто сылаются на конкретные ячейки и ничего сложного из себя не представляют. Кроме трёх диапазонов: arr, x_e, y_e. Можно заметить, что x_e и y_e - это то, на что ссылается ряд данных в диаграмме, и, что это формулы, описывающие кривые, которые я приводил выше. А вот ИД arr надо осмыслить: =СТРОКА( СМЕЩ( Лепота!$A$1; ; ; x) )X у нас равен 5400. Функция СМЕЩ() сформирует диапазон A1:A5400. А формула СТРОКА() будет вычислена для каждой строки данного диапазона, поэтому в результате мы получим массив чисел от 1 до 5400. Этот массив, будучи переданным в x_e, y_e тоже породит соответствующие массивы. Обратите внимание, что arr пропускается через функцию РАДИАНЫ(). Таким образом мы градусы (1..5400) переводим в радианы. Если честно, то я не знал, что ТАК можно :) Вот собственно и всё. А тот макрос, который у меня есть в книге, он просто случайным образом, но плавно меняет параметры R1, R2, D в пределах от From до To с шагом Step. P.S. Любителям WinAPI с его Sleep рекомендую обратить внимание на конструкцию Application.Wait Now + 1 / 24 / 60 / 60 / 2 :) Ну а теперь залипайте дальше на лицезрение циклоид :) | |
| Просмотров: 15492 | Комментарии: 13 | | |
| Всего комментариев: 12 | ||||||||||
| ||||||||||
 Зачем делать столь глубокие выводы на единичных фактах? Я дурачился. Но вы правы в том, что WinAPI я не знаю, но никаких религиозных запретов на этой почве перед собой не воздвигаю. Просто часто sleep - единственное, что видишь у VBA-шников, но в Excel особой необходимости в нем нет. То есть, если вам нужно сделать паузу, то нефиг городить огород с winapi. Файл ваш посмотрел - офигенно. Дома посмотрю подробнее. Вот для этого и winapi не грех применять
Зачем делать столь глубокие выводы на единичных фактах? Я дурачился. Но вы правы в том, что WinAPI я не знаю, но никаких религиозных запретов на этой почве перед собой не воздвигаю. Просто часто sleep - единственное, что видишь у VBA-шников, но в Excel особой необходимости в нем нет. То есть, если вам нужно сделать паузу, то нефиг городить огород с winapi. Файл ваш посмотрел - офигенно. Дома посмотрю подробнее. Вот для этого и winapi не грех применять  , так что лучше прочитать её "по диагонали" и никогда так не делать.
, так что лучше прочитать её "по диагонали" и никогда так не делать. 
